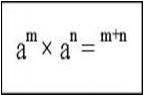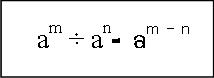ยินดีต้อนรับนักเรียนทุกคนเข้าสู่ Website ห้องเรียนครูนุช
ครูกลุ่มสาระการเรียนรู้คณิตศาสตร์ โรงเรียนวังบ่อวิทยา
อำเภอหนองบัว จังหวัดนครสวรรค์
วันอังคารที่ 19 พฤษภาคม พ.ศ. 2563
เลขยกกำลังที่มีเลขชี้กำลังเป็นจำนวนเต็ม
สมบัติของเลขยกกำลัง
1. สมบัติการคูณเลขยกกำลังที่มีเลขชี้กำลังเป็นจำนวนเต็มบวก เมื่อ a เป็นจำนวนใด ๆ และ m, n เป็นจำนวนเต็มบวก
เช่น 23x 27x 29 = 2 (3 + 7 + 9) = 219
2. สมบัติการหารเลขยกกำลังที่มีเลขชี้กำลังเป็นจำนวนเต็มบวก
กรณีที่ 1 เมื่อ a เป็นจำนวนจริงใดๆที่ไม่ใช่ศูนย์ และ m, n เป็นจำนวนเต็มบวกที่ m > n
เช่น 412÷ 43=412-3 = 49
กรณีที่ 2 เมื่อ a เป็นจำนวนจริงใดๆที่ไม่ใช่ศูนย์ และ m, nเป็นจำนวนเต็มบวกที่ m = n
นิยาม ถ้า a เป็นจำนวนจริงใดๆ ที่ไม่ใช่ศูนย์ a0 = 1
เช่น 67÷ 67 = 67-7 = 60 = 1 หรือถ้า (-7)o = 1
กรณีที่ 3เมื่อ a เป็นจำนวนจริงใดๆที่ไม่ใช่ศูนย์ และ m, n เป็นจำนวนเต็มบวกที่ m < n
เช่น 
= 1/ 54-9
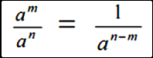
นิยาม ถ้า a เป็นจำนวนจริงใดๆ ที่ไม่ใช่ศูนย์ และ n เป็นจำนวนเต็มบวก แล้ว
หรือ 
เช่น 
หรือ 
3.สมบัติอื่นๆของเลขยกกำลัง
1. เลขยกกำลังที่มีฐานเป็นเลขยกกำลัง
เมื่อ a ≥0 และ m, n เป็นจำนวนเต็ม
เช่น 
2. เลขยกกำลังที่มีฐานอยู่ในรูปการคูณ หรือการหารของจำนวนหลาย ๆจำนวน
และ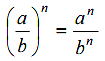 
เมื่อ a ≠ 0 , b ≠ 0 และ n เป็นจำนวนเต็ม
เช่น 
3. เลขยกกำลังที่มีเลขชี้กำลังเป็นเศษส่วน
เมื่อ a > 0 และ n เป็นจำนวนเต็มบวกที่มากกว่า 1
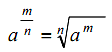เมื่อ a ≠ 0 และ m เป็นจำนวนเต็มบวก ; n ≥ 2
4. 
จำนวนยกกำลัง ศูนย์ ได้เท่ากับ 1
อินเตอร์เซกชัน
ยูเนียน (Union)
บทนิยาม
เซต A ยูเนียนกับเซต
B คือเซตซึ่งประกอบด้วยสมาชิกที่เป็นสมาชิกของเซต A หรือ เซต B หรือทั้ง A และ B
สามารถเขียนแทนได้ด้วย สัญลักษณ์ A ∪ B
ตัวอย่างเช่น A ={1,2,3}
B= {3,4,5}
∴ A ∪ B = {1,2,3,4,5}
อินเตอร์เซกชัน (Intersection)
บทนิยาม
เซต A อินเตอร์เซกชันเซต B
คือ เซตซึ่งประกอบด้วยสมาชิกที่เป็นสมาชิกของเซต A และเซต B สามารถเขียนแทนได้ด้วยสัญลักษณ์ A ∩ B
ตัวอย่างเช่น A ={1,2,3}
B= {3,4,5}
∴A ∩ B = {3}
คอมพลีเมนต์ (Complements)
บทนิยาม
ถ้าเซต A ใดๆ
ในเอกภพสัมพัทธ์ U แล้วคอมพลีเมนต์ของเซต A คือ เซตที่ประกอบด้วยสมาชิกที่เป็นสมาชิกของ U แต่ไม่เป็นสมาชิกของ
A สามารถเขียนแทนได้ด้วยสัญลักษณ์ A'
ตัวอย่างเช่น U = {1,2,3,4,5}
A ={1,2,3}
∴A' = {4,5}
ผลต่าง (Difference)
บทนิยาม
ถ้าเซต A และ B เป็นเซตใดๆในเอกภพสัมพัทธ์ u เดียวกันแล้ว
ผลต่างของเซต A และ B คือ
เซตซึ่งประกอบด้วยสมาชิกที่เป็นสมาชิกของเซต A แต่ไม่เป็นสมาชิกของเซต
B สามารถเขียนแทนได้ด้วยสัญลักษณ์ A - B
ตัวอย่างเช่น A ={1,2,3}
B= {3,4,5}
∴A - B = {1,2}
วันจันทร์ที่ 18 พฤษภาคม พ.ศ. 2563
บทที่ 1 เซต
1.1 เซต
1.2 การดำเนินการระหว่างเซต
1.2.1 อินเตอร์เซกชัน
1.2.2 ยูเนียน
1.2.3 คอมพลีเมนต์
1.2.4 ผลต่างระหว่างเซต
1.3 การแก้ปัญหาโดยใช้เซต
1.2 การดำเนินการระหว่างเซต
1.2.1 อินเตอร์เซกชัน
1.2.2 ยูเนียน
1.2.3 คอมพลีเมนต์
1.2.4 ผลต่างระหว่างเซต
1.3 การแก้ปัญหาโดยใช้เซต
ชั้นมัธยมศึกษาปีที่ ๕
บทที่ 1เลขยกกำลัง
1.1 เลขยกกำลังที่มีเลขชี้กำลังเป็นจำนวนเต็ม
1.2 รากที่ n ของจำนวนเต็ม
1.3 เลขยกกำลังที่มีเลขชี้กำลังเป็นจำนวนตรรกยะ
ชั้นมัธยมศึกษาปีที่ ๔
คณิตศาสตร์ เรื่องเซต
สมัครสมาชิก:
บทความ (Atom)